首先来看看什么是点的压缩。

        椭圆曲线上的任一仿射点(x, y)（非无穷远点）都可以压缩成利用其y坐标的最后一比特（记为y*）和x坐标来表示，即(x, y*)，这就是点的压缩。反过来，利用(x, y*)恢复y坐标，还原仿射点(x, y)的过程就称为点的解压缩。

利用点的压缩可以减少存储和传输时的数据量，但增加了数据处理时间。

        代码中用参数point_conversion_form_t来表示是否进行点压缩，point_conversion_form_t的定义如下：

typedef enum {

        POINT_CONVERSION_COMPRESSED = 2,

        POINT_CONVERSION_UNCOMPRESSED = 4,

        POINT_CONVERSION_HYBRID = 6

} point_conversion_form_t;

其中

1. POINT_CONVERSION_COMPRESSED 的值为 2，表示采用点压缩。

2. POINT_CONVERSION_UNCOMPRESSED的值为4，表示不采用压缩。

3. POINT_CONVERSION_HYBRID的值为6，表示混合使用，即既包含点压缩又包含未压缩。

为了节省资源，一般会用一个字节表示压缩形式和y坐标的最后一个字节（必要时）。假设用form来表示压缩形式，则表示压缩形式和y*的字节buf[0]为：

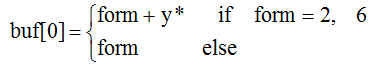。               ………(5.16)

        点的压缩很简单，直接用(x, y*)表示即可。但是怎么解压缩该呢，怎么恢复y坐标呢？简而言之，就是利用Weierstrass方程计算平方根。具体过程如下：

其中，Step2计算可以利用文件bn_sqrt.c中的函数BN_mod_sqrt()实现（函数BIGNUM *BN_mod_sqrt(BIGNUM *in, const BIGNUM *a, const BIGNUM *p)的功能是计算a mod p的平方根）。

利用给定的压缩点(x, y*)来设置点坐标(x, y)的过程其实就是解压缩的过程：

1. point->X ← x

2. point->Y ← 取x3＋ax＋b的某一个平方（由y*决定）

3. point->Z ← 1

其中y*＝1表示y坐标为奇数，y*＝0表示y坐标为偶数。

───────────────────────────────────────

int EC_POINT_set_compressed_coordinates_GFp(const EC_GROUP *group, EC_POINT *point, const BIGNUM *x, int y_bit) 

功能：    利用压缩点坐标来设置点坐标

输入：    group，x【压缩点的x坐标】，int y_bit【y坐标最后一比特】

输出：    point【不压缩的点】

返回：    1【正常】or 0【出错】

出处：    ec_lib.c

调用：     ▼   ec_GFp_simple_set_compressed_coordinates(const EC_GROUP *group, EC_POINT *point, const BIGNUM *x_, int y_bit)

───────────────────────────────────────

代码的处理过程是，先通过解压缩计算出y坐标，然后直接调用设置仿射点坐标的函数EC_POINT_set_affine_coordinates_GFp(group, point, x, y)。

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。